Дифференциальная передача
Друзья!
Мы продолжаем серию публикаций интересных статей из журнала FT:PEDIA, переведённых на русский язык. Сегодня мы познакомимся с дифференциальной передачей.
Журнал: FT:PEDIA 4/2014
Оригинальное название статьи: Das Differentialgetriebe
Автор: Thomas Püttmann
Перевод: Мария Гончарова
Дифференциальная передача
Дифференциальные приводы использовались и продолжают использоваться в различных сферах. Данная статья наглядно разъяснит на примере моделей fischertechnik, как они работают. Это позволит показать на практике, что означает понятие смены системы координат, очень важное для математики, естественных наук и техники.
История
В 1900 г. возле греческого острова Антикитера водолазы нашли остов судна, затонувшего приблизительно в 100 г. до н.э. С этого корабля на поверхность было поднято множество артефактов. Одной из таких находок стал неприметный обломок металла, чье научное и историко-техническое значение было признано общественностью лишь спустя многие десятилетия. Речь шла о частично сохранившемся, невероятно сложном механизме, состоявшем из по меньшей мере 27 зубчатых передач, который использовался для расчета движения Солнца и Луны, а также для предсказания затмений и лунных фаз.

Рис. 1: Дифференциальный привод в том виде, в котором английский историк Дерек де Солла Прайс воссоздал его (вплоть до количества зубцов) по части антикитерского механизма [1]. Современные модели уже не столь точно следуют данной форме.
Сохранившиеся фрагменты совершенно однозначно указывают на то, что в античной Греции эпициклические механизмы ― такие механизмы, в которых кроме обычной передачи движения от одного колеса к другому, некоторые колёса обкатываются вокруг основного колеса (см. рис.1) ― использовались не только в теоретическом моделировании орбит небесных тел, но и в механических передачах. Их существование доказывает, что уже в то время был известен дифференциальный привод с цилиндрической шестерней.
Очень вероятно, что дифференциальный привод использовался в качестве основного механизма в механическом компасе-колеснице Ма Цзюня (ок. 200-265 г.), но данное предположение основывается лишь на упоминании в письменном источнике. Действующих образцов из древнего Китая не сохранилось, прежде всего потому, что каждая новая правящая династия зачастую уничтожала все, что было создано во время правления предшествующей династии.

Рис. 2: Предполагаемая модель компаса-колесницы, воссозданная Джорджем Ланчестером, Лондонский научный музей (Фото: Andy Dingley CC BY 3.0)

Рис. 3: Модель Ланчестера из деталей fischertechnik
Первое достоверно известное применение дифференциального привода было зафиксировано в часах. В 18 веке истинное солнечное время, т.е. время, которое показывали солнечные часы, еще считалось достаточно значимым. Механические часы показывали среднее солнечное время. Чтобы вычислить по их данным истинное солнечное время, на часы зачастую наносились таблицы коррекции. Лондонский часовщик Джозеф Уильямсон в 1720 году впервые использовал дифференциальный привод для механической коррекции [2]. А другому ученому-часовщику впервые пришла в голову идея использовать дифференциальную передачу в автомобильных приводах. В 1748 известный своими механическими игрушками изобретатель Жак де Вокансон (1709-1782) продемонстрировал Людовику XV автомобиль с приводом на все колеса и дифференциальной передачей, приводимый в движение с помощью большого часового механизма. В 1827 году дифференциальная передача для парового самоходного грузовика была запатентована еще одним часовых дел мастером ― Онесифором Пекье (1792-1852). Об использовании дифференциальной передачи в автомобилях подробно рассказывается в видеофильме «Around the Corner», вышедшем в 1937 году. Дифференциальные передачи в автомобилях сначала использовались в качестве распределительного механизма, т.е. с их помощью приводился в движение только один из трех приводных блоков/валов; распределение крутящего момента на каждый вал происходило за счет движения по кривой.

Рис.4: Модель автомобильного привода Дирка Фокса из деталей fischertechnik
В конце 19-го первой половине 20 веков дифференциальные приводы широко применялись в механических аналоговых вычислительных машинах. Стоит посмотреть очень информативный, хотя и имеющий явную военную направленность, учебный фильм «Basic Mechanisms in Fire Control Computers» (Основные механизмы в системах управления огнем), снятый в 1953 году.
Примеры
Вначале рассмотрим несколько примеров. На рис.5 представлены самый первый дифференциальный привод от fischertechnik, еще из «серо-красного» периода, и современный дифференциальный привод. Они оба работают за счет маленьких конических шестерен, а сам механизм скрыт в корпусе. Поэтому они не годятся для того, чтобы наглядно продемонстрировать функционирование такого привода.

Рис.5: Дифференциальные приводы в наборах fischertechnik
Прекрасный образец дифференциального привода с очень удобным для демонстрации дифференциальным корпусом создал Дирк Фокс (см. рис.4 и 6). Здесь также использованы небольшие конические шестерни. Дифференциальный привод, изображенный на рис.7, я разработал специально для того, чтобы максимально наглядно объяснить принцип его работы. Он хорошо подходит для использования в компасе-колеснице или аналоговом компьютере, но менее пригоден для автомобилестроения.

Рис. 6: Дифференциальный привод с коническими шестернями, разработанный Дирком Фоксом

Рис. 7: Дифференциальный привод с зубчатыми передачами
На рис.8 и 9 представлены другие примеры дифференциального привода, на которых я хотел бы объяснить основные принципы, из которых следует исходить при разработке таких приводов для конкретных целей с использованием конструктора fischertechnik или же без него. Дальнейшие примеры конструкций вы можете найти в фотогалерее ft-сообщества.

Рис. 8: Дифференциальный привод с зубчатой цилиндрической передачей для использования в компасе-колеснице или аналоговом компьютере

Рис. 9: Дифференциальный привод с зубчатой цилиндрической передачей, пригодный к использованию также и в автомобилестроении
Эксперименты
Если вы хотите получить полное представление о том, как функционирует дифференциальный привод, вам нужно собрать функциональные модели, изображенные на рис.7 и 10. Вращательные движения верхней шестерни, водила и нижней шестерни связаны между собой, т.е. каждый из трех приводных блоков/валов не может приводиться в движение независимо от других. Можно выбрать два блока и повернуть в желаемое положение, третий повернется в установленную позицию сам. Такая взаимосвязь трех крутящих моментов вокруг общей оси характерна для планетарной коробки передач. Чтобы понять, как осуществляется это взаимодействие, мы рекомендуем вам промаркировать белым цветом зубец на верхней и нижней шестерне таким образом, чтобы оба промаркированных зубца и водило были расположены на одной линии с пазом на красной детали модели (рис.10).

Рис. 10: Маркировка шестерен
Эксперимент 1: Мы удерживаем водило неподвижно и начинаем вращать нижнюю шестерню. Вращательное движение посредством колеса водила передается на верхнюю шестерню. Она начинает поворачиваться на такое же расстояние, что и нижняя, но в противоположном направлении. При этом совершенно неважно, какой размер имеет колесо водила.

Рис. 11: Неподвижное водило
Эксперимент 2: Поместим модель снова в исходную позицию, теперь вместо водила будем удерживать в неподвижном положении нижнюю шестерню, а верхнюю при этом поворачивать. Колесо водила будет вращаться в том же направлении, но лишь на половину заданного угла. Это второе важное наблюдение. Этот факт объяснить не так просто, как наблюдение из первого эксперимента. К нему мы еще вернемся позже

Рис. 12: Зафиксированная нижняя шестерня
Характеристика дифференциальных приводов
При изготовлении дифференциальных приводов крайне важно придерживаться следующего принципа: планетарная коробка передач будет являться дифференциальным приводом в том случае, если при остановке одного любого ее элемента (приводного блока/вала) она проявляет себя как в рассмотренных выше экспериментах. Иначе говоря: мы выбираем один из элементов и останавливаем его. Тогда два других элемента будут совершать вращение на определенный угол. Если третий элемент поворачивается в том же направлении лишь на половину от траектории вращения первого, или же вдвое дальше при вращении в противоположном направлении, то речь идет о дифференциальном приводе. Конечно же, имеет смысл выбрать тот элемент для остановки, на примере которого легче всего объяснить взаимосвязь между двумя другими элементами. Мы поясним этот принцип с помощью нескольких примеров.
В качестве первого примера рассмотрим антикитерский привод, изображенный на рис.1. Если мы будем удерживать неподвижно поворотный диск со звеньями Z41 [3] и начнем вращение вокруг металлической оси, то оба элемента Z10, а также красный Z15 с зажимной муфтой будут синхронно поворачиваться. Оба черных Z15 также начинают синхронно поворачиваться, но в противоположном направлении. Таким образом, этот привод является дифференциальным.
Во-вторых, рассмотрим привод с рис.8. Водило имеет неподвижное соединение с черной пластмассовой осью. Остановим его. Если мы теперь будем поворачивать правую металлическую ось, а вместе с ней и Z20 на определенный угол, что оба Z10 сместятся на вдвое большее расстояние, но в противоположном направлении, также как и внешние Z15, прочно соединенные с ними посредством валов. Оба внешние элемента Z15, свободно вращающиеся вокруг черной оси, двигаются таким образом в том же направлении, что и Z20, но проходят вдвое большее расстояние. Это означает, что данный привод также является дифференциальным.
Подобным же образом дело обстоит и в случае с зубчатой передачей на рис.9. При остановленном водиле оба элемента Z15 вращаются в том же направлении, что и Z20, но проходят лишь половину расстояния. То есть, и в этом случае речь идет о дифференциальном приводе. Отличие от предыдущего привода с зубчатой передачей состоит в том, что теперь пластмассовая и металлическая оси вращаются в противоположном направлении, если внешние элементы Z15 находятся в зафиксированном положении. Этот вариант, как мы видим, подходит для автомобилестроения: Приводящее усилие поступает на красный Z15, колеса достаточно большого размера могут быть прикреплены к обеим осям ― в случае необходимости оси можно удлинить.
Математическое описание
Давайте попробуем описать состояния, в которых может находиться дифференциальный привод, с помощью математического уравнения и, таким образом, поясним на простейшем практическом примере понятие смены системы координат. Первый шаг по направлению к математическому описанию состоит в точном обозначении связанных величин и однозначном определении способа их измерения. Если сэкономить время на данном этапе, в дальнейшем будут возникать неточности.

Рис. 13: Угол x
Связанными величинами являются угол вращения водила и углы вращения обеих шестерен. Задавая параметры угла необходимо обязательно указать, относительно чего ведется измерение и в каком направлении вращения. Мы будем измерять угол по отношению к прямой линии, которая проходит от центральной оси через паз красного блока 30, против часовой стрелки значение будет положительным, по часовой стрелке отрицательным, при этом мы смотрим на модель сверху. Эти три угла x, y и z представлены на рис.13 и 14.
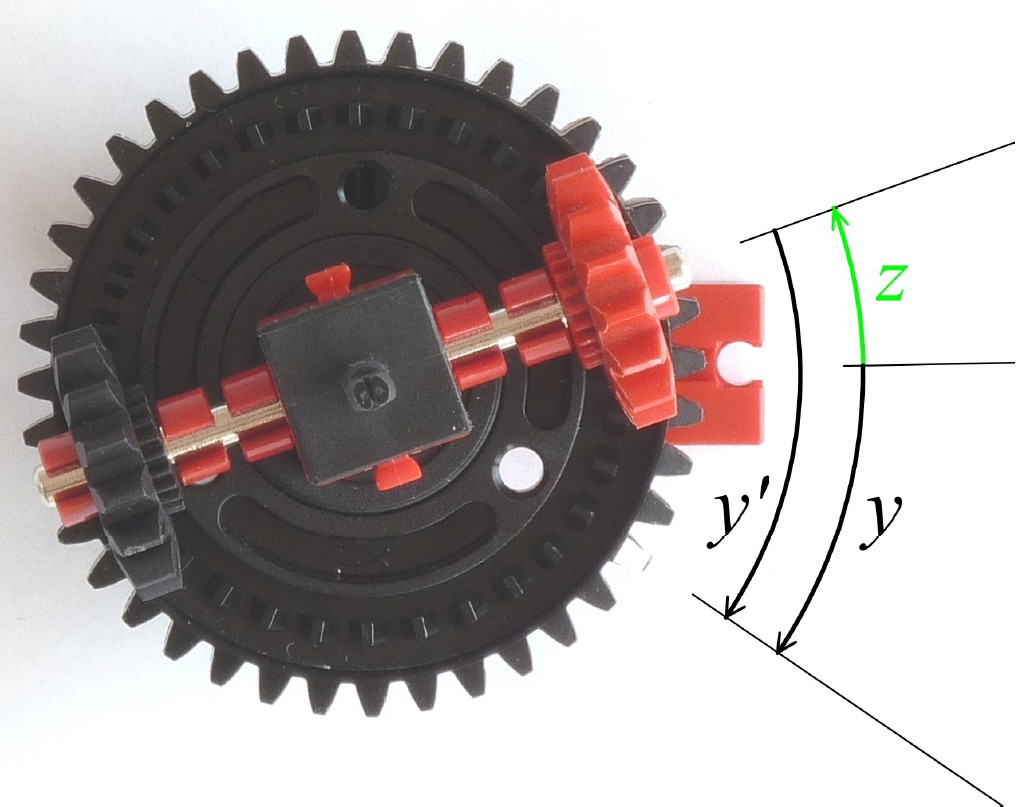
Рис. 14: Углы y и z
В нашем первом эксперименте мы останавливали водило. Данное действие мы опишем уравнением z=0. Мы выявили и объяснили, что в этом случае вращением верхней солнечной шестерни вызвано вращение на такое же расстояние в противоположном направлении. Более точно с математической точки зрения это можно выразить уравнением y = -x или эквивалентно:
x + y = 0
Этим уравнением можно описать все состояния привода при остановленном водиле.
Во втором эксперименте мы наблюдали, как при зафиксированной нижней шестерне, т.е. y = 0, водило проходит вдвое меньший путь, чем верхняя солнечная шестерня. Уравнение
x = 2z
описывает, таким образом, все состояния привода при остановленной нижней шестерне. Этому уравнению нет прямого объяснения. Но еще менее понятным представляется нам до сих пор общий случай (рис.15).

Рис. 15: Общее состояние дифференциального привода
Смена наблюдателя
Представим, что существует некий наблюдатель, который вращается вместе с водилом и измеряет угол относительно положения водила, а не относительно прямой линии, проходящей от центральной оси через паз красного блока 30. Этот наблюдатель измеряет три угла z’=0, x’ и y’. Поскольку с его точки зрения колесо водила также связывает движение обеих шестерен между собой, то x’ = — y’ или эквивалентно этому
x’ + y’ = 0.
Теперь основным вопросом будет, как соотносятся друг с другом измеренные нами углы x, y и z и измеренные движущимся вместе с водилом наблюдателем углы x’, y’ и z’. Для того, чтобы это увидеть, повернем обе шестерни и водило вместе на угол -z против часовой стрелки, т.е. на угол z по часовой стрелке. Водило, таким образом, вновь оказывается в исходном положении. Измерим теперь углы x’ и y’, которые до этого были измерены движущимся наблюдателем. Получаем, что x’ = x-z, а y’= y-z. Включение этих двух формул в уравнение x’ + y’ = 0 дает нам [4]:
x + y -2z = 0
Это основное уравнение дифференциальной передачи. Оно описывает все её возможные состояния. Оно наглядно демонстрирует, что вращательное движение водила вычисляется посредством усреднения вращательных движений обеих шестерен. Справедливость данного уравнения можно проверить по рис.13, 14 и 15.
С помощью данного уравнения мы можем еще раз вернуться к нашему второму эксперименту. Там мы останавливали нижнюю шестерню, что описано с помощью уравнения y = 0. Далее мы описывали все возможные состояния привода с помощью уравнения x = 2z. Таким образом мы математически обосновали наше наблюдение.
Планетарный привод
Приведенные выше размышления можно обобщить с помощью универсального планетарного привода. Проиллюстрируем это на примере стандартного планетарного привода с колесом с внутренними зубцами (рис.16).

Рис. 16: Планетарный привод
Здесь мы также имеем три угла: угол x солнечной шестерни, угол y колеса с внутренними зубцами и угол z водила, все три угла измеряются относительно одной общей полуоси, на которой они могут быть расположены. В данном случае также проще всего можно понять принцип работы привода, остановив водило. Состояния привода в таком случае можно описать с помощью уравнения
x = -3y,
т.к.соотношение зубцов 10:30, и происходит смена направления вращения. Наблюдатель, вращающийся вместе с водилом, измеряет значение углов x’ и y’, соответствующих уравнению x’ = -3 y’.
Взаимосвязь между нашими углами и углами, полученными движущимся наблюдателем можно представить с помощью уравнений x’ = x-z и y’= y-z, как и в приведенном выше примере. Методом подстановки получаем следующее уравнение:
x + 3y — 4z = 0
Оно описывает все возможные состояния привода.
Для каждого планетарного привода аналогично можно вывести уравнение в форме
n₁ · x + n₂ · y +n₃ · z = 0
Это уравнение называется уравнением Уиллиса. Поскольку все три приводных блока можно постоянно вращать синхронно, то все значения x, y и z при условии x = y = z будут являться решением к данному уравнению. Из этого следует, что n₁ + n₂ +n₃ = 0.
Анонс
В следующем номере мы планируем уделить более пристальное внимание теме компасов-колесниц. При этом мы планируем использовать представленные в данной статье приводы и основные идеи. В дальнейшем мы планируем рассказать об использовании дифференциальных приводов в механических аналоговых вычислительных машинах. Наши сегодняшние размышления наводят на мысль, что линейные системы уравнений можно решать при помощи приводов и подсказывают, как это делается. В действительности, эта идея уже не раз приходила в головы и даже печаталась в различных источниках, однако она так и не нашла убедительного воплощения. Для установки коэффициентов необходимы точные настраиваемые вариативные передачи. До сих пор подходящей концепции для этого нет. Однако для сложения и вычитания отдельных величин в сложных механизмах дифференциальные приводы использовались довольно широко.
О построении моделей
К сожалению, не все зубчатые колеса Z15 (артикул 35695) могут бесперебойно работать на осях. Нужно искать наиболее удачные комбинации из собственного запаса деталей, чтобы получить хорошо работающий привод. В приводах, представленных на рис.1, 8 и 9, использованы зубчатые колеса Z15 (артикул 37685), которые в сегодняшних наборах fischertechnik больше не встречаются. Но их можно без проблем заменить на свободно вращающийся Z15, в который можно воткнуть свернутый трубочкой кусок бумаги, а затем ось. Кусок бумаги в идеале должен иметь длину, достаточную для охвата 4-миллиметовой оси, чтобы ось была расположена точно по центру.
В конце статьи приводим список деталей для конструирования дифференциального привода, представленного на рис.7:
| Кол-во | Артикул | Наименование |
| 2 | 31022 | Зубчатое колесо Z40 |
| 2 | 31058 | Гайка ступицы цанговой |
| 2 | 68535 | Ступица свободного хода чёрная |
| 2 | 130593 | Ось с концевиком |
| 1 | 32064 | Блок 15 с отверстием |
| 1 | 31032 | Металлическая ось 60 |
| 6 | 37679 | Стопорное кольцо |
| 2 | 35695 | Зубчатое колесо Z15 |
Источники
[1] Derek de Solla Price: Gears from the Greeks. Transactions of the American Philosophical Society, Vol. 64, Part 7, 1974.
[2] Henry C. King: Geared to the Stars. The Evolution of Planetariums, Orreries, and Astronomical Clocks. University of Torronto Press, Torronto, Buffalo, 1978.
[3] fischertechnik: Hobby 2, Motor und Getriebe. Fischer-Werke, Tumlingen, 2/1975.
[4] Thomas Püttmann: Zahnräder und Übersetzungen (Teil 2). ft:pedia 3/2011, S. 25-28.



